Poseidon Sponge Bugs in ArkWorks
Avoiding Cryptographic Failures in Hashing
We found two subtle yet impactful bugs in the ArkWorks library’s implementation of the Poseidon Sponge. This discovery highlights the complexity and precision required in cryptographic implementations. In this article, we’ll first explain what Poseidon Sponge is, how it works, and then delve into the two bugs we uncovered.
What is Poseidon Sponge?
Poseidon is a hash function using the principle of a sponge. It can absorb inputs (elements to hash), and squeeze outputs (hashed elements). The values that we squeeze depend directly on the values that we absorb.
The inputs and outputs are field elements (they are values modulo another value). We can create a “bonus” function which absorb elements of another field, or bytes, for example. We just have to convert this data into elements of the initial field.
Why use it?
Poseidon is widely used in Zero-Knowledge Proof domain (and by extension in SNARK/STARK/Blockchain domain) because of its compatibility with cryptography “types”, like finite field elements, and its efficiency.
Ed: Poseidon has also an advantage in the use. In ZKP, there is a principle named Fiat-Shamir heuristic, consisting of replacing the randomness of certain values with the hash of all previous values. It allows us to transform an interactive protocol (with random values) into a non-interactive protocol (with hashed values). To be sure that there are no flaws in the protocol using this heuristic, we must hash every previous values, and why not some parameters etc. This can be difficult to manage, we have to be sure that we forgot nothing each time we want a new hashed value etc. With the principle of sponge, we can keep it throughout the protocol without worrying about having to put all the right parameters back each time.
In terms of hashing functions, we can cite SHA-256, which is largely used for its speed and security, but in ZKP domain, we more often use finite field elements, and converting them into bits (the input of the SHA hash) is very expensive. We can also cite Pedersen wich is another hashing function used in ZKP, but, because it works with Elliptic Curves, this function may not be as efficient as Poseidon. Finally, we can cite MiMC and Rescue, two other hash sponges designed for ZKP, but both a little less efficient than Poseidon.
How it works?
Poseidon is not a “classical” hash function where you hash some values, and get a fixed-size output. Using the sponge construction, we can input as many values to hash as we want, and recover as much hashed values as we want. The operation of inputting values to hash is called absorb(), and the operation of recovering hashed values is called squeeze().
There are several possible constructions for a sponge, and we have, among others, the Simplex construction, and the Duplex construction. ArkWorks uses the Duplex construction, but we will explain first what is the Simplex construction to better understand the Duplex construction. Before entering in the details, let’s take a look on what the two constructions have in common.
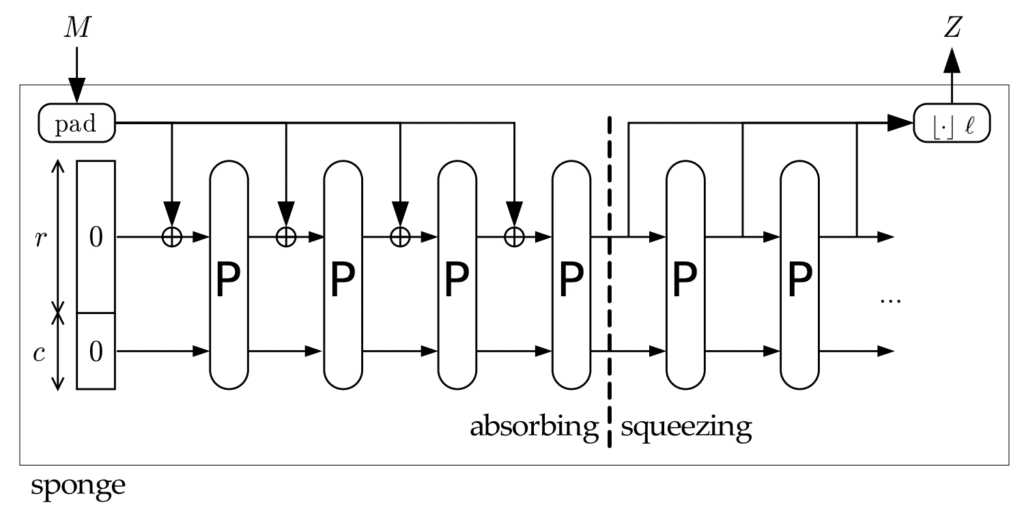
The Poseidon sponge principle
In Poseidon, when we absorb N field elements, we do not absorb directly every element. We consider successively only a certain number of field elements (defined in parameters) that we treat, until we’ve treated them all. We call this number of elements that can be treated at once the rate r of the sponge.
In the same way, when we squeeze I elements, we consider in fact blocks of r elements (and not directly the I elements).
The Poseidon sponge contains a vector of field elements, of size r+c, called state, and initially filled with 0. absorb modifies this internal state, and squeeze outputs certain values of the state. Between (almost) every call to absorb() and squeeze(), we apply a function P (permute()) on (all) the state. This function mixes the state pseudo-randomly-like to propagate differences. The security of the sponge depends on this function P (how well it mixes).
The Simplex and the Duplex construction don’t have the same use! With the Simplex construction, once we have squeeze(), we can’t absorb() anymore. It’s a one-shot function (but we can absorb() as much as we want if it is before the squeeze()). With the Duplex construction, we can absorb() and squeeze() in the order we want, as much as we want.
The Simplex construction
In the Simplex construction, absorb() an input consists of
- Chunking the input into r-length sections
- Adding the first r-length section to the r first elements of the internal
state(terms-to-terms) - Applying
permute()on all thestate - Repeating with the following r-length section
If the input length is not a multiple of the rate r, one can think to pad this input to have the right length, but we don’t talk about it here.
And squeeze() I elements consists of
- Recovering the r first elements of the
state - Applying
permute()on all thestate - Repeating until recovered (just more than) I elements
- Truncating the recovered values to keep just I values
- Outputting the truncated value
The Duplex construction
In the Duplex construction, we don’t have directly the absorb() and squeeze() functions. Instead, we have what we call duplex(), that takes in parameters
- σ : a vector of elements (as
absorb()function) of length r - I: a non-negative integer ≤ r
duplex() consists of
- Adding the input σ to the r first elements of the internal
state(terms-to-terms) - Applying
permute()on all thestate - Recovering the r first elements of the
state - Truncating the recovered values to keep just I values
- Outputting the truncated value
Again, if the input length is not the rate r, one can think to pad this input to have the right length, but we don’t talk about it here
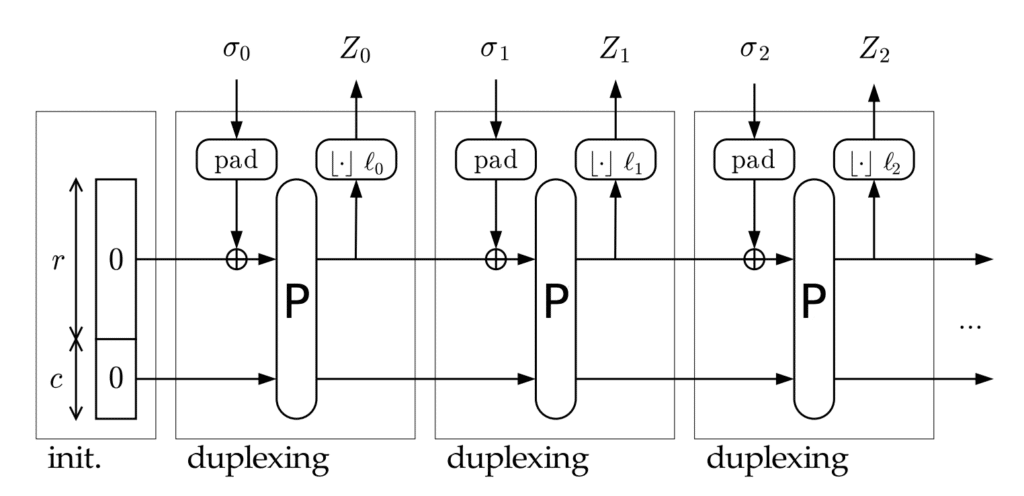
We can simulate absorb() on an input of arbitrary length by
- Chunking the input into r-length sections
- Calling
duplex()on each r-length input, with I=0
If the input length is not a multiple of the rate r, one can think to pad this input to have the right length, but we don’t talk about it here.
Another way to manage the problem is to consider that we wait squeeze() to pad, in the sense that if we have two (or more) absorb() one after the other, then the values of the next absorb() can complete the missing values of the previous absorb() to raise r values in total, and so it is less expensive to wait the last call to absorb() to pad (the last call to absorb() is the one just before a call to squeeze(), it is why it can be managed in the squeeze() function).
We have illustrated the principle previously explained so that you have a good intuition (this is not a rigorous protocol, just an example):

We can simulate squeeze(n) by
- Calling
duplex()with σ = Ø and I=r until there are less than r elements tosqueeze - Calling
duplex()with σ = Ø and I the remaining number of values tosqueeze
We can do as for absorb(), if we call several times in a row the squeeze() function: instead of forgetting the excess values in the truncation step, we can stock them, and if one calls again squeeze() just after, we first output the values that we have stored and, if needed, we apply the classic squeeze() function with the remaining number of values.
We have illustrated the principle previously explained so that you have a good intuition (this is not a rigorous protocol, just an example):
The bugs
We are coding a differential fuzzer that allows us to compare the results of protocols, implemented by different libraries. For the Poseidon case typically, we compare the implementations of arkworks, aleo, the custom one of starknet and lambdaworks, and the one of aztec is currently being integrated.
In another project, we already find a bug in January, and this differential fuzzer allows us to find this bug again, and another one in the same protocol. These bugs are coming from the arkworks library (especially the one implementing Poseidon).
bad_if_cond_poseidon_squeeze
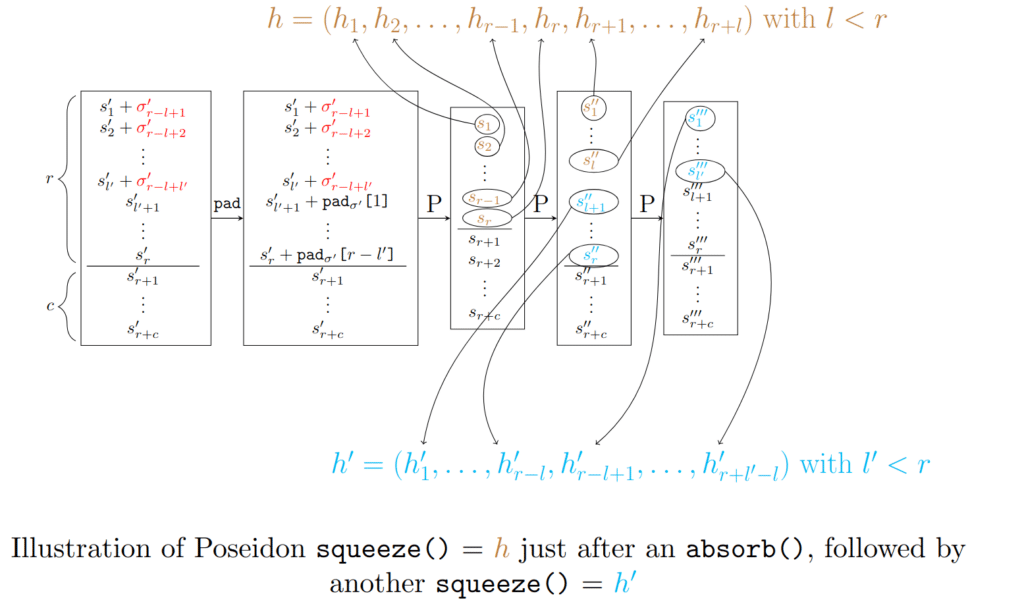
As mentioned above, when we squeeze elements, we output r values of the state successively, and between each r outputted values, we permute(). The problem here is that there is a case where we don’t permute(). Indeed, due to the line 178, we permute() only when the number of remaining elements to squeeze is not the rate r. So, if we first squeeze() I values with 0 < l < r, and then we squeeze() after that r values, the last I outputs of the second squeeze() will be the same as the I squeezed values of the previous squeeze() because the second squeeze() will first output the values of the first squeeze() which have not been squeezed (the r-I last values of the state), check the number of values to squeeze() (which is the rate r since the length of the output vector has not been changed – it is done line 182), and permute or not following the result of the comparison. In our case, the comparison leads to not permute() (since the length of the output vector is r), and so we enter in the first if loop line 160 without permute() before. We literally recover the values of the state (which are the same as before), and return it.
We represented the error in the following schemes:
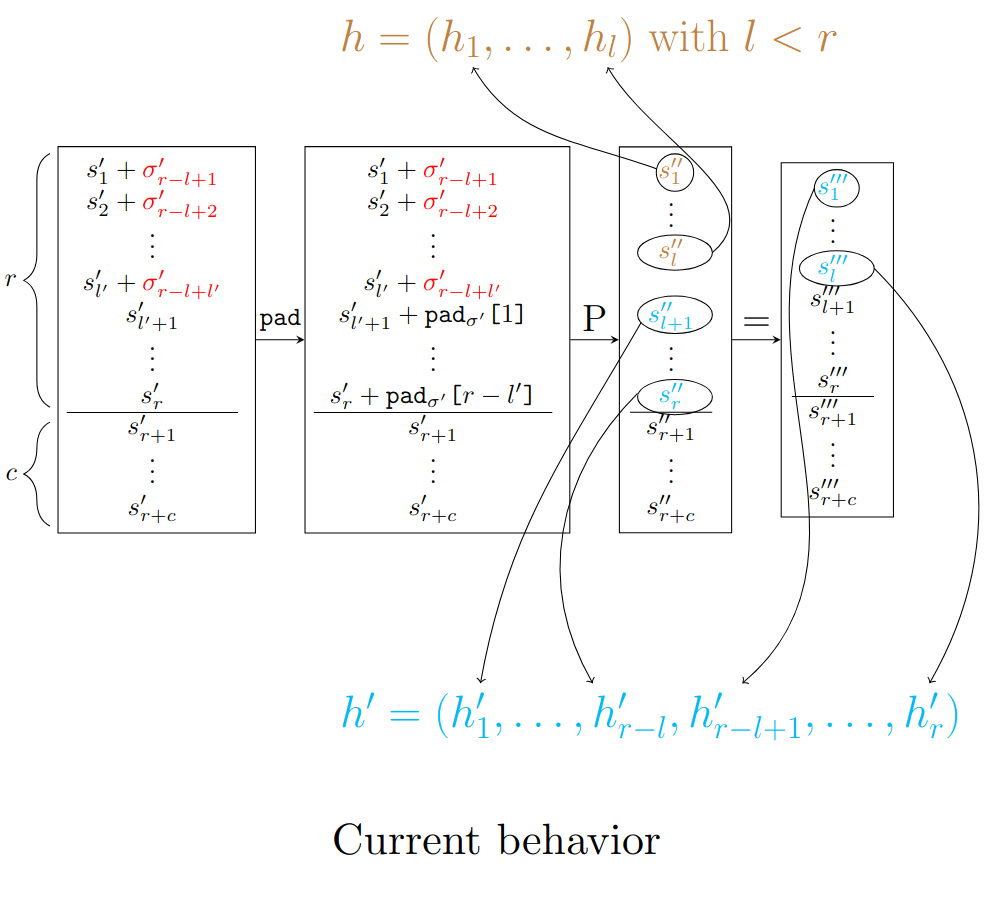
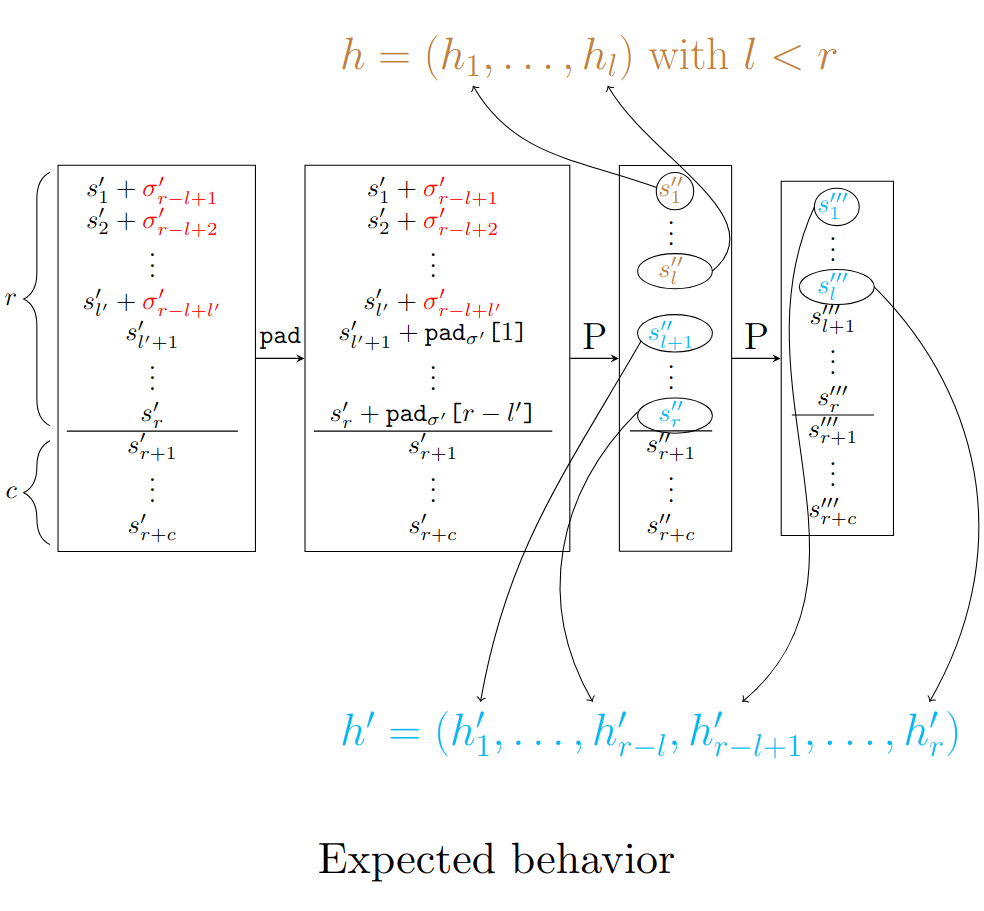
squeeze_0
This error is very simple to understand. What happens if we squeeze() 0 elements? The instinctive and logical answer is that nothing is happening, i.e. there is no permutation (the internal state of the sponge remains intact) and no element is output.
But in the current implementation, calling squeeze (squeeze_native_field_elements in the code) on 0 right after an absorb results in a permutation on the internal state (instead of doing nothing).
Conclusion
The discovery of these two bugs in the Arkworks implementation of Poseidon Sponge underscores the critical need for precision in cryptographic systems. Cryptographic libraries, even those widely trusted, are not immune to subtle implementation errors, which can lead to significant consequences for the systems that rely on them.
By leveraging differential fuzzing across multiple implementations, we have exposed flaws in ArkWorks and potential vulnerabilities elsewhere. This methodology is proving invaluable in uncovering hidden issues and ensuring the robustness of cryptographic protocols.
These findings are likely the tip of the iceberg. As we continue our analysis, we anticipate uncovering more unexpected behaviors in implementations. This reinforces the need for rigorous testing and validation as the cornerstone of cryptographic security.
References
- Bertoni, G., Daemen, J., Peeters, M., & Van Assche, G. (2020). Cryptographic Sponge Functions (CSF), Version 0.1. Keccak Team. Retrieved from https://keccak.team/files/CSF-0.1.pdf
- Grassi, L., Rechberger, C., Ronen, E., & Schofnegger, M. (2019). POSEIDON: A New Hash Function for Zero-Knowledge Proof Systems. IACR Cryptology ePrint Archive. Retrieved from https://eprint.iacr.org/2019/458.pdf
- Arkworks Contributors. (2023). Poseidon Sponge Implementation in Rust. Arkworks Crypto-Primitives GitHub Repository. Retrieved from https://github.com/arkworks-rs/crypto-primitives
Patrick Ventuzelo / @Pat_Ventuzelo
Ronan Thoraval / @RonanThoraval
About Us
Founded in 2021 and headquartered in Paris, FuzzingLabs is a cybersecurity startup specializing in vulnerability research, fuzzing, and blockchain security. We combine cutting-edge research with hands-on expertise to secure some of the most critical components in the blockchain ecosystem.
Contact us for an audit or long term partnership!