Grehack ctf WRITEUP
Casting reverse challenge into cryptanalysis challenge
In mid-November, I participated in the GreHack CTF with my team (Phreaks 2600), and the challenge I will present was one of the problems featured in the competition. Interestingly, only two other teams managed to solve it, this makes it a particularly intriguing challenge, categorized under “reverse“.
- Category: Reverse
- Solves: 3
- Info provided: 1 binary file (ELF 64-bit LSB executable dynamically linked and stripped)
- Flag:
GH{Y0u_m4d3_L4gR4nG3_L4u6h_H4rD}
Reversing
main function implements a password-checking mechanism with a mathematical twist.
When executed, the program first prints a welcoming message introducing the challenge, followed by prompts to input three coefficients: a[0], a[1], and a[2]. These coefficients are stored in specific memory locations and are critical for validating the password.
After this setup, the program expects the user to supply a password as a command-line argument. If no password is provided, it informs the user of the correct usage and exits. However, if a password is supplied, the program processes it character by character.
For each character in the password, the program uses a custom function, FUN_00400706, to compute a reference value. This function takes the character’s position (or index) as an input and calculates a value based on a series of iterations involving the coefficients provided earlier.

The program compares each character of the password with the computed reference value. If they match, a counter is incremented. Once all characters are processed, the program checks two conditions to determine if the password is valid: the number of matches must equal the number of characters processed, and the password must have exactly 33 characters. If these conditions are satisfied, a success message is displayed. Otherwise, it informs the user that the password is invalid.
The function FUN_00400706 is central to this process. It calculates reference values by iterating 33 times and combining the coefficients with the input index. The result depends heavily on the coefficients, but only the first three are user-defined during execution. The remaining coefficients are already embedded in the program (starting from 0x00401aec).


So, the challenge revolves around recovering the first three coefficients (a[0], a[1], and a[2]) because the remaining coefficients are already known. Once these three coefficients are correctly identified, they can be input into the program, and the function FUN_00400706 can be executed to compute the reference values for each index from 0 to 32. By combining these values, the entire password can be reconstructed character by character. The task is therefore to deduce the initial coefficients, input them, and then use the program logic to retrieve the correct password.
Let’s rewrite the FUN_00400706 in python and translate the problem into a more mathematical form
The function FUN_00400706 can be described as a polynomial evaluation function operating within a finite field. Mathematically, it computes:
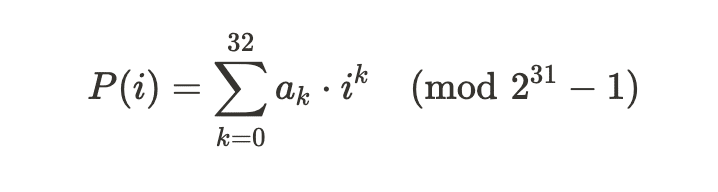
where:
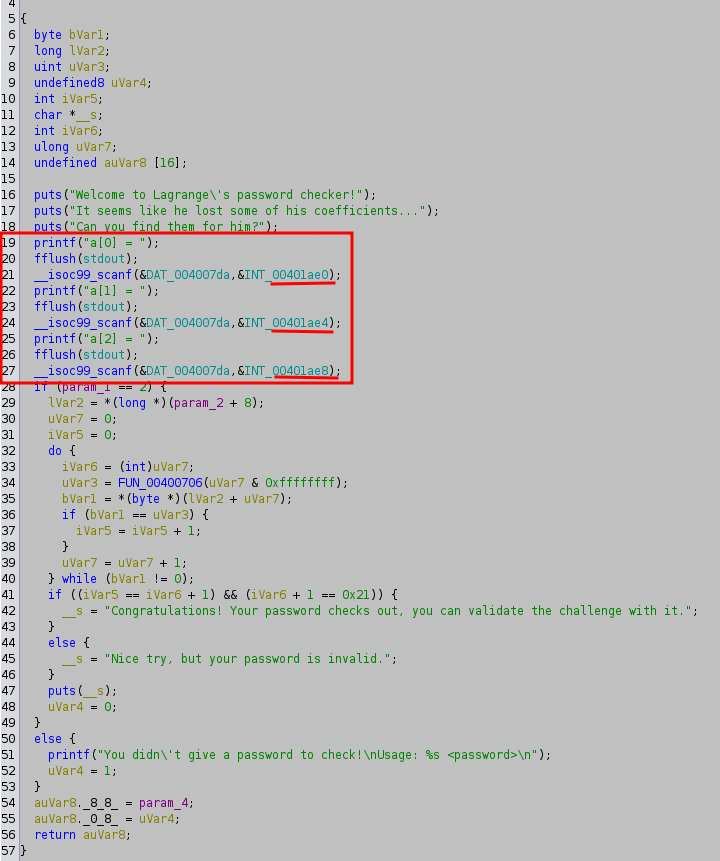
i(orparam_1in the decompiled code) is the input to the function,a_kare the coefficients stored in the arrayINT_00401ae0,2^31 - 1 = 0x7FFFFFFFis the modulus defining the finite field.
This is the python (with sagemath) re-implementation:
p = 0x7FFFFFFF
F = FiniteField(p)
def eval_at(i, coeffs):
s = 0
for power, c in enumerate(coeffs):
s += (i**power)*c
return int(F(s))
Therefore, let’s rewrite P(i) in a splitted form to separate it into two distinct sums: one for the first three coefficients (unknown) and another for the rest (known).
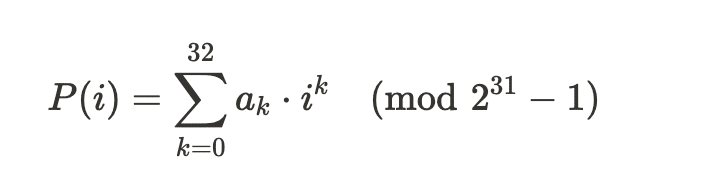
We can split the sum into two parts:
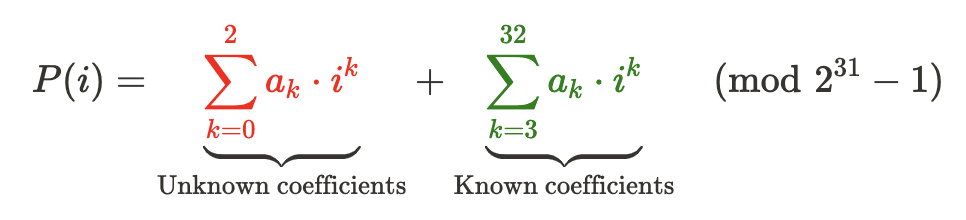
Here:
- The first sum involves the coefficients
a_0, a_1anda_2which are unknown. - The second sum involves the remaining coefficients, which are known because they are hardcoded in the program.
In practice:
- We denote the unknown part as
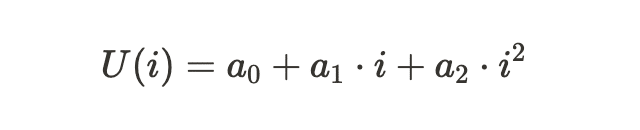
And the known part as .
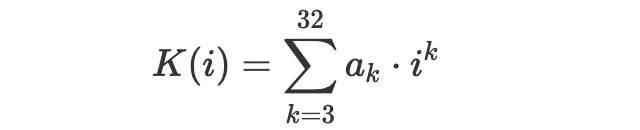
Thus, P(i) can be written as:

In this form, the problem becomes clear: we know K(i) because the coefficients a_3 to a_32 are available, but we must deduce U(i) (and hence a_0, a_1, a_2) to reconstruct the full password.
Exploitation time
Before proceeding with the exploitation, it’s important to recall a key detail: the format of the flag. We know that the flag starts with GH{, and based on the decompiled code with the puts function, the password we are tasked to find corresponds directly to this flag. This knowledge is crucial because it gives us the starting values of the password’s first three characters, which we can leverage to deduce the unknown coefficients.
The function get_known_value , calculates the known part (ie. K(i)), based on the higher-order coefficients (from a_3 to a_32).
def get_known_value(i, coeffs):
s = 0
power = 3
for _, c in enumerate(coeffs):
s += (i**power)*c
power += 1
return F(s)
Using this, we construct a system of equations based on the known first three characters of the flag. Each character’s ASCII value provides a corresponding P(i) for i = 0, 1, 2 . Y will represents an array containing the ASCII values of the first three characters of the flag ('G', 'H', '{'), converted to elements in our finite field F.
(Note: Remember that the i values correspond to the index of the character in the password).
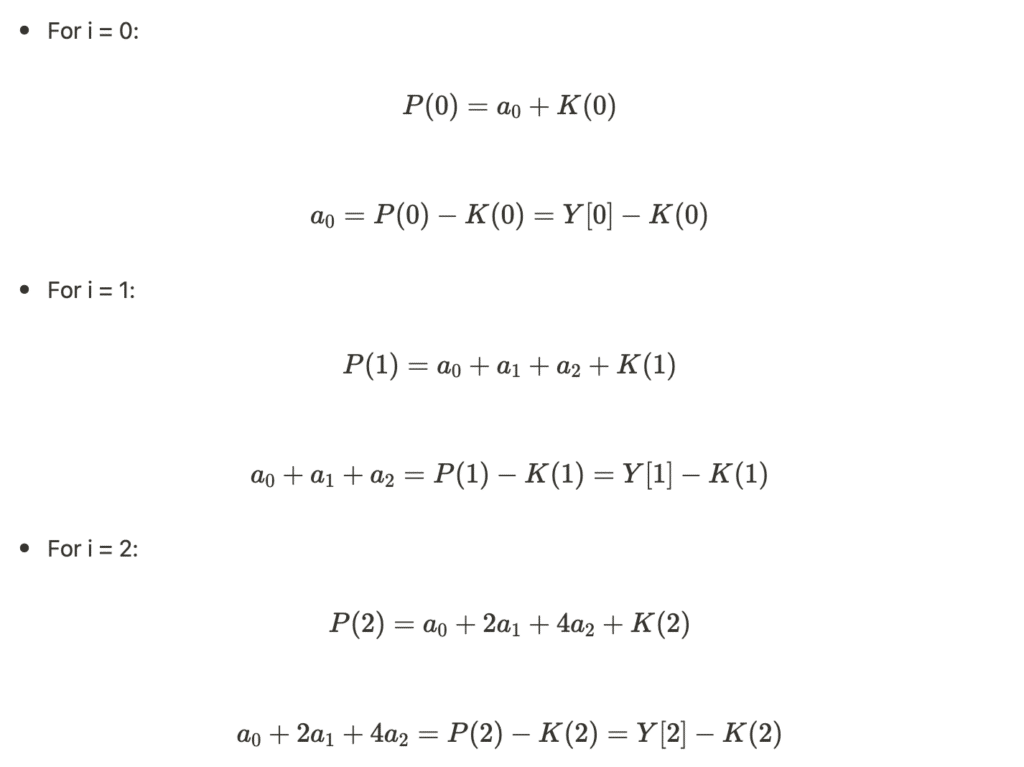
Finally, we obtain a system of linear equations in F:
- From
P(0): We directly geta₀ - From
P(1): We geta₀ + a₁ + a₂ - From
P(2): We geta₀ + 2a₁ + 4a₂
Python code:
Y = [F(ord("G")), F(ord("H")), F(ord("{"))]
a0 = Y[0] - get_known_value(0, coeffs)
a0_plus_a1_plus_a2 = F(Y[1] - get_known_value(1, coeffs))
a0_plus_2_a1_plus_4_a2 = F(Y[2] - get_known_value(2, coeffs) )
Therefore, solving this system reveals our unknown coefficients (a₀, a₁, a₂), allowing us to fully reconstruct P(i) and ultimately recover the complete flag.
Let’s express our system of equations in matrix form:
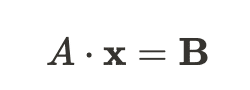
Where:
Ais our coefficient matrix based on character positionsx = [a0, a1, a2]ᵀcontains our unknown coefficientsBholds our previously calculated values
The system is represented by these matrices:
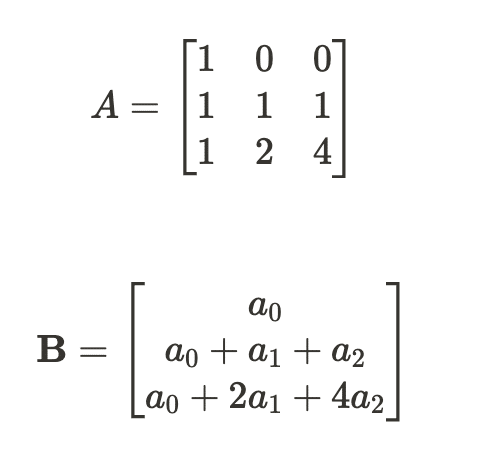
To find our unknowns, we can solve:
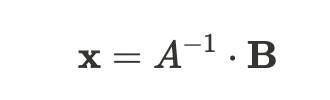
(A is invertible over the finite field F)
Note: with sagemath you can directly use solve_right to get x (link)
Final Exploit
from sage.all import *
p = 0x7FFFFFFF
F = FiniteField(p)
coeffs = [ 0x4df125f9,
0x287d857f, 0x4c95eeda, 0x34ccabc4, 0x57c8eb71,
0x14ea06b2, 0x2f1548a8, 0x0726b2a5, 0x03bcc6dc,
0x2b2db70a, 0x35586ad0, 0x034630e5, 0x6cd02785,
0x1af8bbef, 0x511622ce, 0x04278620, 0x5ab7041e,
0x23e0396f, 0x3d60c00d, 0x2c4ad7a3, 0x0bd8c6db,
0x67ef8970, 0x31328955, 0x41407fa9, 0x7702b717,
0x73a17921, 0x05321672, 0x26e9a468, 0x3f0278e9,
0x074706c4
]
coeffs = list(map(F, coeffs))
def get_known_value(i, coeffs):
s = 0
power = 3
for _, c in enumerate(coeffs):
s += (i**power)*c
power += 1
return F(s)
Y = [F(ord("G")), F(ord("H")), F(ord("{"))]
assert sum(coeffs) % p == get_known_value(1, coeffs)
a0 = Y[0] - get_known_value(0, coeffs)
a0_plus_a1_plus_a2 = F(Y[1] - get_known_value(1, coeffs))
a0_plus_2_a1_plus_4_a2 = F(Y[2] - get_known_value(2, coeffs) )
A = Matrix(F, [ [1, 0**1, 0**2],
[1, 1**1, 1**2],
[1, 2**1, 2**2]])
B = vector(F, [a0, a0_plus_a1_plus_a2, a0_plus_2_a1_plus_4_a2])
assert A.is_invertible()
solution = A**-1 * B # or solution = A.solve_right(B)
coeffs = list(map(int, solution)) + coeffs
def eval_at(i, coeffs):
s = 0
for power, c in enumerate(coeffs):
s += (i**power)*c
return int(F(s))
r = []
for i in range(33):
r.append(chr(eval_at(i, coeffs)))
print(solution)
print("".join(r))

Patrick Ventuzelo / @Pat_Ventuzelo
Dimitri Carlier / @Ectari0
About Us
Founded in 2021 and headquartered in Paris, FuzzingLabs is a cybersecurity startup specializing in vulnerability research, fuzzing, and blockchain security. We combine cutting-edge research with hands-on expertise to secure some of the most critical components in the blockchain ecosystem.
Contact us for an audit or long term partnership!



